题目链接
思路
转化为寻找一个空点,使得这个空点周围2k-1内损失的金块是最少的问题。
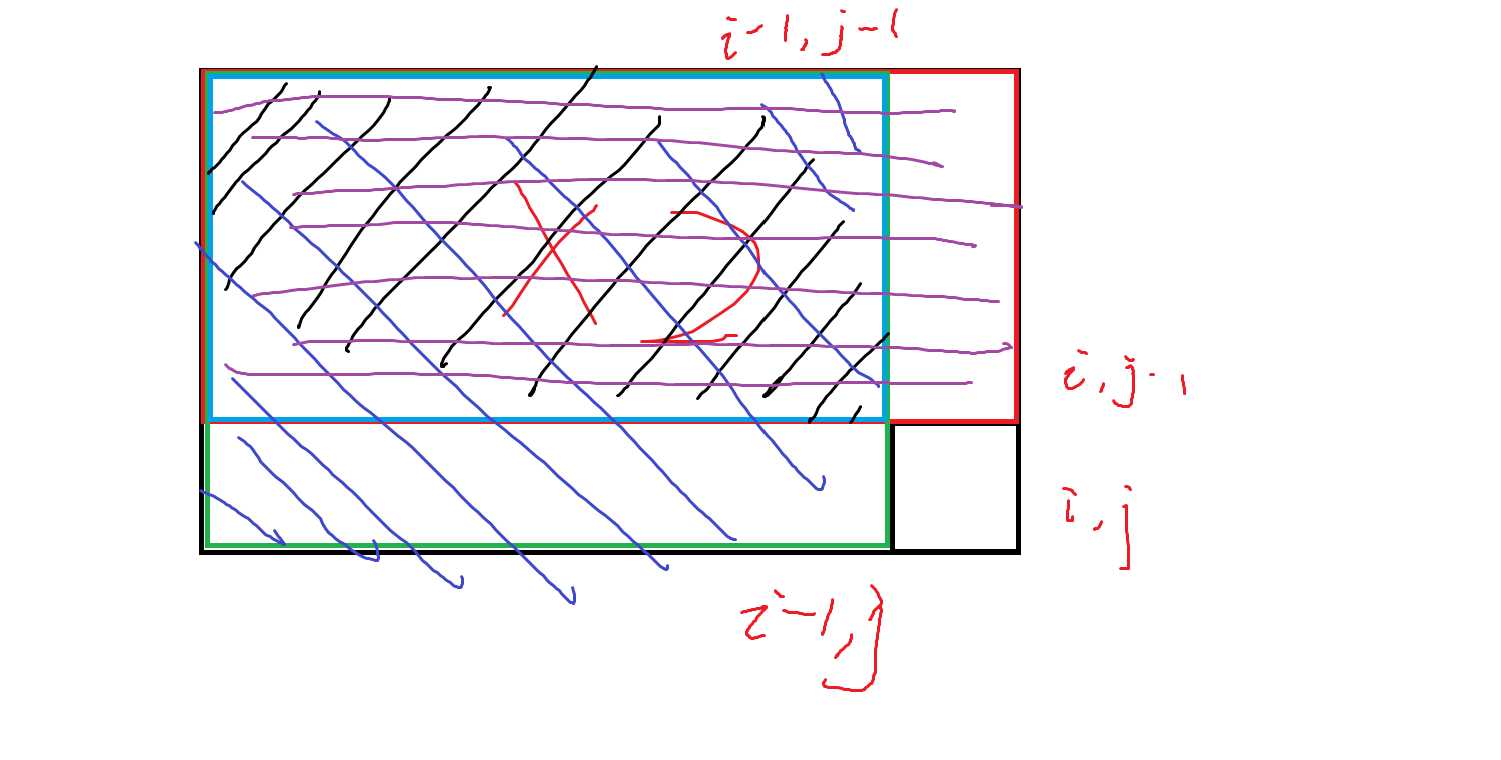
使用二维前缀和存储从(0,0)到当前点位的金块数量。
根据容斥原理,f[i][j] = f[i][j - 1] + f[i - 1][j] + f[i - 1][j - 1]。
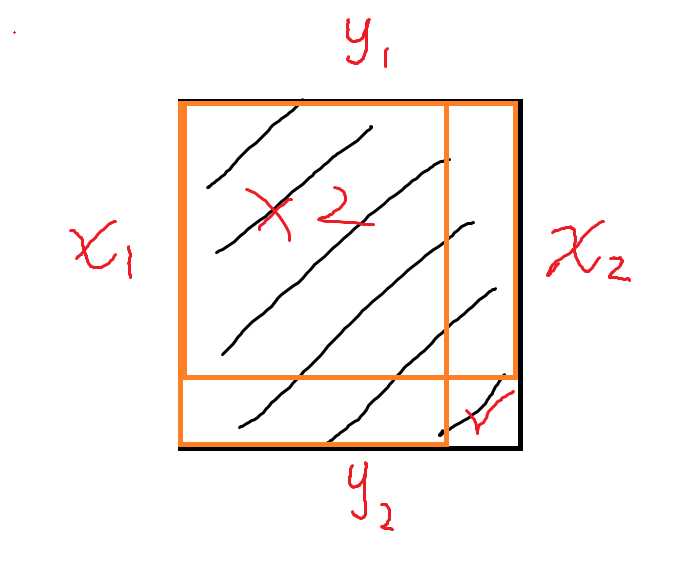
寻找最小金块损失点。以(i, j)为中心,向四周扩展k格,形成一个边长2k+1的正方形。
同时进行边界处理。
min(res,f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1])
代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <climits>
#include <utility>
#include <cmath>
#include <stack>
#include <queue>
#include <iomanip>
#include <numeric>
#include <bitset>
#include <cstdlib>
#include <set>
#include <map>
#include <unordered_map>
using namespace std;
using ll = long long int;
using ld = long double;
using ull = unsigned long long int;
/*
*/
#define akitama return 0
/*
Author: Akitama
Date: 2025-07-20 16:51:11
Akitama Default Contest Template V2.0
*/
#define vi vector<int>
#define vll vector<ll>
#define pii pair<int, int>
#define pb push_back
#define fi first
#define se second
#define l(x) x << 1
#define r(x) x << 1 | 1
constexpr int N = 1e5 + 7;
constexpr int MOD = 1e9 + 7;
constexpr int INF = 0X3f3f3f3f;
void solve() {
int n, m, k;
cin >> n >> m >> k;
vector<string> a(n);
for (auto &i : a) cin >> i;
if (k == 1) {
ll ans = 0;
for (int i = 0; i < n; ++ i) {
for (int j = 0; j < m; ++ j) {
ans += a[i][j] == 'g' ? 1 : 0;
}
}
cout << ans << endl;
return;
}
vector<vi> f(n + 1, vector<int>(m + 1, 0));
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= m; ++ j) {
f[i][j] = a[i - 1][j - 1] == 'g' ? 1 : 0;
f[i][j] += f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];
}
}
// Find
int res = n * m;
for (int i = 0; i < n; ++ i) {
for (int j = 0; j < m; ++ j) {
if (a[i][j] == '.') {
// i k
// NO out of bound
int x1 = max(1, i - k + 2);
int x2 = min(n, i + k);
int y1 = max(1, j - k + 2);
int y2 = min(m, j + k);
if (x1 > x2 || y1 > y2) continue;
res = min(res,f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]);
}
}
}
cout << f[n][m] - res << endl;
}
signed main() {
cin.tie(nullptr)->ios::sync_with_stdio(false);
int _ = 1; cin >> _;
while (_--){
solve();
}
akitama;
}


Comments NOTHING