牛客寒假算法训练营第四场 H题

题目描述

比赛原因，暂时不公布。

思路分析

f(a, b, c, st) 为当前还剩 a 个 'a'，b 个 'b'，c 个 'c'，上一组组合的后两个珠宝状态为 st = x * 3 + y 时，能够达到的最大喜爱值。
设 x = st / 3, y = st % 3（上一组合的最后两个字符），我们可以选择 a, b, c 作为下一个字符：

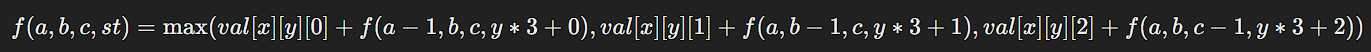
边界条件 当a，b，c都为0时，最后一个组合计算最终值：

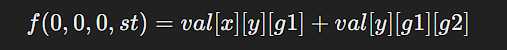
其中，g1,g2是最前面的两个珠宝。

状态数O(n^3)，转移O(3)，总复杂度O(3 \times n ^3) \approx O(n ^ 3)。

代码

#include <bits/stdc++.h>
using namespace std;

#define akitama return 0
#define ll long long

ll val[3][3][3];
int g1, g2;

inline int cti(char c) { return c - 'a'; }
inline char itc(int i) { return 'a' + i; }

struct DP {
    int A, B, C, BD, CD;
    vector<ll> dp;
    vector<int> ch;

    DP(int A_, int B_, int C_) : A(A_), B(B_), C(C_) {
        int sz = (A+1) * (B+1) * (C+1) * 9;
        dp.assign(sz, LLONG_MIN);
        ch.assign(sz, -1);
    }

    inline int idx(int a, int b, int c, int st) {
        return (((a * (B+1) + b) * (C+1) + c) * 9) + st;
    }

    ll f(int a, int b, int c, int st) {
        int p = idx(a, b, c, st);
        if(dp[p] != LLONG_MIN) return dp[p];
        if(a == 0 && b == 0 && c == 0) {
            int x = st / 3, y = st % 3;
            return dp[p] = val[x][y][g1] + val[y][g1][g2];
        }
        int x = st / 3, y = st % 3;
        ll mx = -LLONG_MAX;
        int opt = -1;
        if(a > 0) {
            ll t = val[x][y][0] + f(a-1, b, c, y*3+0);
            if(t > mx) { mx = t; opt = 0; }
        }
        if(b > 0) {
            ll t = val[x][y][1] + f(a, b-1, c, y*3+1);
            if(t > mx) { mx = t; opt = 1; }
        }
        if(c > 0) {
            ll t = val[x][y][2] + f(a, b, c-1, y*3+2);
            if(t > mx) { mx = t; opt = 2; }
        }
        ch[p] = opt;
        return dp[p] = mx;
    }

    string r(int a, int b, int c, int st) {
        string res;
        while(a > 0 || b > 0 || c > 0) {
            int p = idx(a, b, c, st);
            int l = ch[p];
            res.push_back(itc(l));
            int y = st % 3;
            st = y * 3 + l;
            if(l == 0) a--;
            else if(l == 1) b--;
            else c--;
        }
        return res;
    }
};

pair<ll, string> solve(int f1, int f2, int A, int B, int C) {
    DP d(A, B, C);
    int st = f1 * 3 + f2;
    ll sc = d.f(A, B, C, st);
    string seq = d.r(A, B, C, st);
    return {sc, seq};
}

void solve() {
    int n, m;
    cin >> n >> m;
    string s;
    cin >> s;
    int cnt[3] = {0, 0, 0};
    for(char c: s) cnt[cti(c)]++;
    for (int i = 0; i < 3; i++)
        for (int j = 0; j < 3; j++)
            for (int k = 0; k < 3; k++)
                val[i][j][k] = 0;
    for (int i = 0; i < m; i++) {
        string t;
        ll v;
        cin >> t >> v;
        val[cti(t[0])][cti(t[1])][cti(t[2])] = v;
    }
    if(m == 0) {
        cout << 0 << "\n";
        string out;
        out.append(cnt[0], 'a');
        out.append(cnt[1], 'b');
        out.append(cnt[2], 'c');
        cout << out << "\n";
        return;
    }
    ll mx = -LLONG_MAX;
    string res;
    bool fnd = false;
    for (int f1 = 0; f1 < 3; f1++) {
        for (int f2 = 0; f2 < 3; f2++) {
            int c[3] = { cnt[0], cnt[1], cnt[2] };
            c[f1]--;
            c[f2]--;
            if(c[0] < 0 || c[1] < 0 || c[2] < 0) continue;
            g1 = f1; g2 = f2;
            pair<ll, string> p = solve(f1, f2, c[0], c[1], c[2]);
            ll sc = p.first;
            string arr;
            arr.push_back(itc(f1));
            arr.push_back(itc(f2));
            arr += p.second;
            if(sc > mx) {
                mx = sc;
                res = arr;
                fnd = true;
            }
        }
    }
    if(!fnd) {
        mx = 0;
        string out;
        out.append(cnt[0], 'a');
        out.append(cnt[1], 'b');
        out.append(cnt[2], 'c');
        res = out;
    }
    cout << mx << "\n" << res << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T; cin >> T;
    while(T--) {
        solve();
    }
    akitama;
}